Dijkstra Algoritması

Dijkstra algoritması, örneğin yol ağlarını temsil edebilen bir grafikteki düğümler arasındaki en kısa yolları bulmak için bir algoritmadır. Bilgisayar bilimcisi Edsger W. Dijkstra tarafından 1956’da tasarlandı ve üç yıl sonra yayınlandı. Algoritma birçok varyantta mevcuttur.

Dijkstra algoritması en kısayolu belirlerken Greedy(Açgözlü) yaklaşımını kullanır. Yani bir düğümden diğer bir düğüme geçerken olası en iyi yerel çözümü göz önüne alır. Her seferinde bir sonraki düğüme ilerleme Greedy yaklaşımına göre yapılır.

Dijkstra(G,w,s)                            //Başlat
{
     for(each u ∈ V)  
     {
           d[u]= ∞;
           colur[u]=white;
     }
     d[s]=0;
     pred[s]=NIL;
     Q = (tüm köşeler kuyruk);
     
     while (Non-Empty(Q))        //Tüm köşeleri işle.
     {
           u=Extract-Min(Q);       //Yeni köşe bul.
           for (each v ∈ Adj[u] )
                 if(d[u] + w(u, v) < d[v])
                 {
                         d[v] = d[u] + w(u,v);
                         Azaltma-Anahtarı(Q, v, d[v]);
                         pred[v] = u;
                 }
           color[u] = black;
     }
}

Bu algoritmanın çalışmasını örnek bir şekil( graph ) üzerinden göstermeye çalışacağım. Bu gösterimin ardından Dijkstra algoritmasının başarısını ve eksik taraflarını tartışabiliriz.

Aşama 0:

Örneğimizde başlangıç düğümü (node) olarak s düğümünü seçtiğimizi düşünelim ve algoritmanın çalışmasını bu düğümden başlayarak gösterelim.

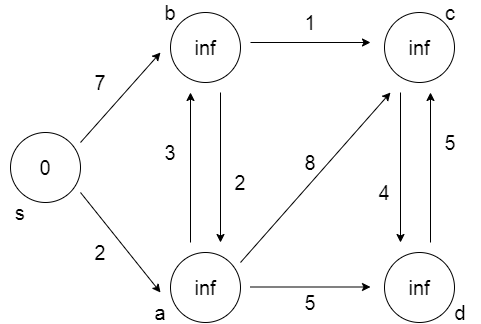
Algoritma başlangıçta bütün düğümlere henüz erişim olmadığını kabul ederek sonsuz ( ∞) değeri atar. Yani başlangıç durumunda henüz hiçbir düğüme gidemiyoruz.

Aşama 1:

Ardından başlangıç düğümünün komşusu olan bütün düğümleri dolaşarak bu düğümlere ulaşım mesafesini güncellenir.

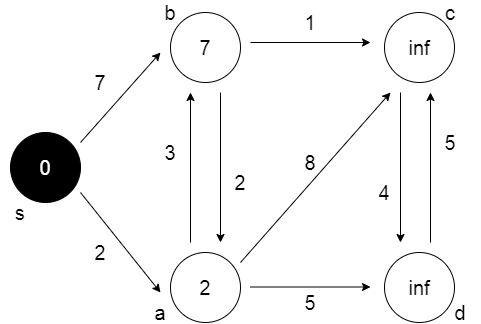
Adj[s]= {a,b}, a ve b üzerindeki düğümleri güncellenir.

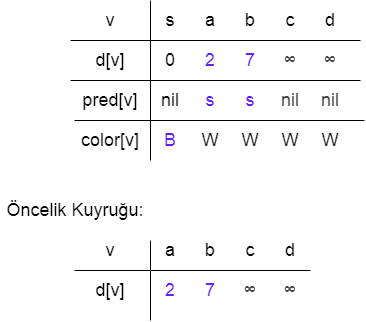
Bu güncelleme işleminden sonra güncellenen düğümlerin komşularını günceller ve bütün düğümler güncellenene ve şekil üzerinde yeni bir güncelleme olmayana kadar bu işlem devam eder.

Aşama 2:

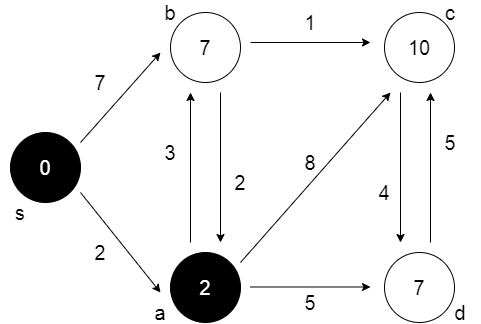
Aşama 1’den sonra, a öncelik kuyruğunda minimum değere sahiptir. Adj[a]= {b, c, d} olarak, b, c, d üzerinde çalışın ve bilgileri güncelleyin.

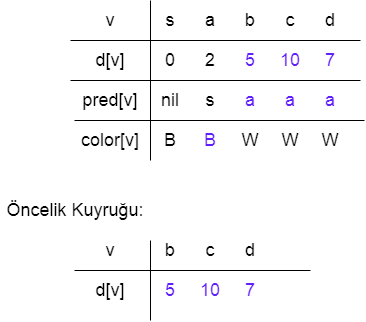
Aşama 3:

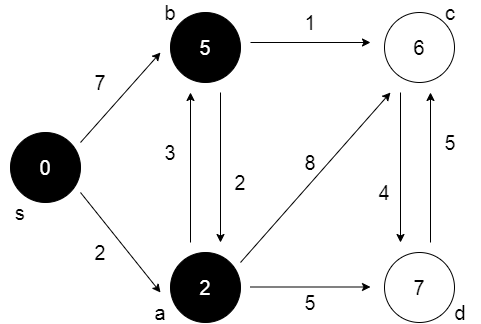
Aşama 2’den sonra, b öncelik kuyruğunda minimum anahtara sahiptir. Adj[b] = {a, c} olarak a, c üzerinde çalışın ve bilgileri güncelleyin.

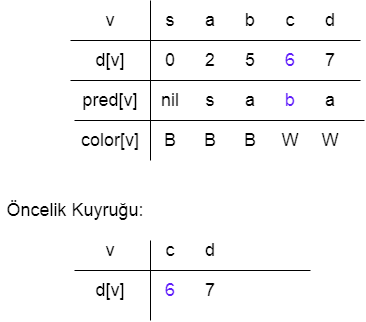
Aşama 4:

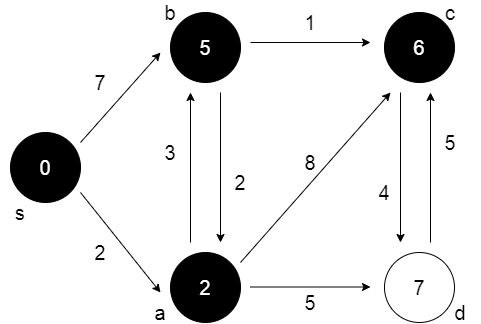
Aşama 3’den sonra, c öncelik kuyruğunda minimum anahtara sahiptir. Adj[c] = {d} olarak, d üzerinde çalışın ve bilgileri güncelleyin.

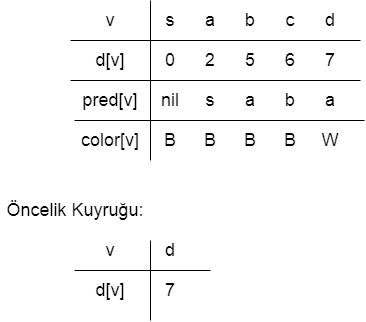
Aşama 5:

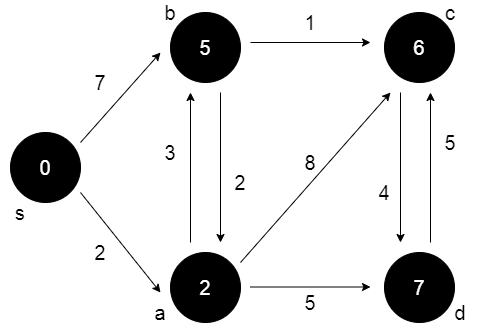
Aşama 4’den sonra, d öncelik kuyruğunda minimum anahtara sahiptir. Adj[d] = {c} olarak, c üzerinde çalışın ve bilgileri güncelleyin.

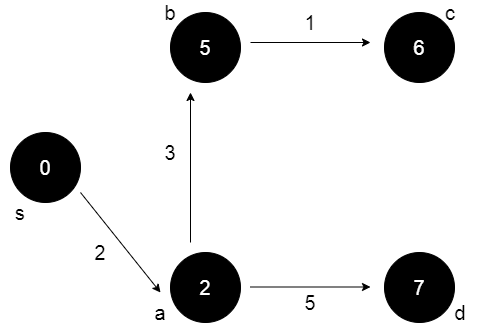
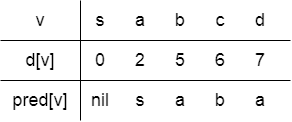
En Kısa Yol Ağacı:

T = (V, A),

A = {(pred[v], v) | v ∈ V \ {s}}

Pred[d] dizisi ağacı inşa etmek için kullanılır.

Dijkstra Algoritmasının Zayıf Yönü

Dijkstra Algoritması’ nın eksi (-) değer taşıyan bir kenar bulunması halinde başarılı çalışmaz. Bunun sebebi eksi (-) değerdeki kenarın sürekli olarak mevcut durumdan daha iyi bir sonuç üretmesi ve algoritmanın hiçbir zaman için kararlı hale gelememesidir.

Kaynakça: Zafercomert, Bilgisayarkavramlari, Codingame, CPalgorithms, Hackerearth