Sıralama Algoritmaları (Sorting Algorithms)

Sıralama algoritmaları kullanmamızdaki amaç, algoritmanın isminden de anlaşılacağı üzere sahip olduğumuz veriyi en hızlı şekilde büyükten küçüğe ya da küçükten büyüğe bir sıraya sokmak. Bunun için kullanılan bir çok sıralama algoritması vardır. Bazısı çok hızlı ama yazımı zor, bazısı az sayıda veri için çok hızlı, bazısının da yazması kolaydır.

Herhangi bir sayıdaki tip verilerin sınırlı bellek ve işlem gücü ile belirli bir sıraya göre dizilmesinin sağlanmasıdır. Burada önemli olan en optimum bellek ve performans ikilisini verecek bir algoritmanın elde edilmesidir.

Sıralama algoritmalarının bazı kriterlere göre sınıflandırılabiliriz:

• Bellek Kullanımı: Çalışırken ek bellek ihtiyacı duyan algoritmalarda kullanılabilecek bir ölçüttür buna ek olarak ayrıca da sıralama işleminin yapılması sırasında hafızanın kullanımına göre de sıralama algoritmaları; Harici sıralama (External Sort) ve Dahili Sıralama (Internal Sort).
• Hesaplama Karmaşıklığı: Oluşturulmuş olan algoritmanın yaptığı işlem sayısının genel bir yapı ile ifade edilmesidir. Temel üç grup ölçek kullanılır. Bunlar en iyi (best), ortalama (average) ve en kötü (worst) durumu olarak belirtilir. İşlem yoğunluğu zaman işleyişiyle paralel olduğundan (ne kadar çok işlem yapılırsa o kadar uzun süre geçer) algoritmanın işleyiş süresini de etkiler.
• Yerdeğiştirmenin Karmaşıklığı: İçerisinde ek bellek kullanmayan (in place) algoritmalarda kullanılan karşılaştırılabilmesi için önemli bir ölçüttür.
• Durağanlık(stability): Algoritmanın uygulanması sırasında sıralanmış bir verinin tekrar sıralamaya tabi tutulup tutulmadığını belirten ölçektir.
• Rekürsiflik: İç içe kendi kendini çağıran algoritmalarda kullanılan bir ölçüttür. Burada en önemli kriter stack dediğimiz maksimum iç içe çağırım kapasitesine dikkat edilmesi ve bu kapasitenin kullanılma sıklığıdır.

Fakat en önemli kriterler

• Hafıza Verimliliği (Memory efficiency)
• Zaman Verimliliği (Time efficiency)

Algoritma analizindeki iki önemli kriteri bunlardır. Bir algoritmanın hızlı çalışması demek daha çok hafızaya ihtiyaç duyması demektir. Tersi durumda da bir algoritmanın daha az yere ihtiyaç duyması daha yavaş çalışması demektir. Bir algoritma hem zaman hem de hafıza olarak verimliyse bu durumda diğer algoritmalardan başarılı sayılabilir.

Aşağıda bazı sıralama algoritmaları verilmiştir:

1. Seçerek Sıralama (Selection Sort)

Selection Sort (Seçerek Sıralama) aslında performans bakımından diğer sıralama algoritmalarına kıyasla bir tık zayıf kalsa da zor durumlarımızda bize yardımcı oluyor. Uygulaması oldukça basit olan bu algoritma dizinin ilk elemanının en küçük eleman olduğunu varsayıyor. Ardından tek tek bu elemanı diğer elemanlarla karşılaştırıyor. Eğer karşılaştırdığı eleman daha küçük ise onu en küçük değer olarak alıyor ve ilk eleman yerine artık diğer elemanları onunla karşılaştırıyor. Dizinin sonuna vardığında ise en küçük elemanı dizinin başına yazıyor. Ardından bu işlemi 2. elemandan başlayarak yapıyor ve bulduğu en küçük değeri 2. sıraya koyuyor benzer şekilde işlemi dizinin son elemanına kadar aynı şekilde tekrarlıyor. Selection Sort’un kodlaması kısmı ise şu şekilde :

for i in range(len(arr)):
    enKucukId = i
    for j in range(i+1,len(arr)):
        if arr[j] < arr[enKucukId]:
            enKucukId = j      
    arr[i],arr[enKucukId] = arr[enKucukId], arr[i]

2. Kabarcık Sıralaması (Bubble Sort)

Dizinin elemanları üzerinden ilk elemandan başlayarak ve her geçişte sadece yan yana bulunan iki eleman arasında sıralama yapılır. Dizinin başından sonuna kadar tüm elemanlar bir kez işleme tabi tutulduğunda dizinin son elemanı (küçükten büyüğe sıralandığında) en büyük eleman haline gelecektir. Bir sonraki tarama ise bu en sağdaki eleman dışarıda bırakılarak gerçekleştirilmektedir. Bu dışarıda bırakma işlemi de dış döngüdeki sayaç değişkeninin değerinin her işletimde bir azaltılmasıyla sağlanmaktadır. Sayaç değişkeninin değeri 1 değerine ulaştığında ise dizinin solunda kalan son iki eleman da sıralanmakta ve sıralama işlemi tamamlanmaktadır.

for i in range(len(arr)-1):
    for j in range(0,len(arr)-i-1):
        if arr[j] > arr[j+1]:
            arr[j], arr[j+1] = arr[j+1],arr[j]

3. Eklemeli Sıralama (Insertion Sort)

Yerleştirerek sıralama işlevi belirli bir anda dizinin belirli bir kısmını sıralı tutarak ve bu kısmı her adımda biraz daha genişleterek çalışmaktadır. Sıralı kısım işlev son bulunca dizinin tamamına ulaşmaktadır. Elemanların sırasına uygun olarak listeye tek tek eklenmesi ile gerçekleştirilen sıralamadır.

for i in range(1,len(arr)):
    deger = arr[i]
    j = i-1
    while(j>= 0 and deger < arr[j]):
        arr[j+1] = arr[j]
        j -= 1
    arr[j+1] = deger

4. Birleştirme Sıralaması (Merge Sort)

Verinin hafızada sıralı tutulması için geliştirilen sıralama algoritmalarından bir tanesidir. Basitçe sıralanacak olan diziyi ikişer elemanı kalan parçalara inene kadar sürekli olarak ikiye böler daha sonra bu parçaları kendi içlerinde sıralayarak birleştirilir. Sonuçta elde edilen dizi sıralı dizinin kendisidir. Bu açıdan bir parçala fethet (divide and conquere) yaklaşımıdır. Sıralı iki veri grubunu birleştirerek üçüncü bir sıralı veri grubu elde etmeye dayanır.

def merge(sol, sag):
	if not len(sol) or not len(sag):
		return sol or sag
	sonuc = []
	i, j = 0, 0
	while (len(sonuc) < len(sol) + len(sag)):
		if sol[i] < sag[j]:
			sonuc.append(sol[i])
			i+= 1
		else:
			sonuc.append(sag[j])
			j+= 1
		if i == len(sol) or j == len(sag):
			sonuc.extend(sol[i:] or sag[j:])
			break 
	return sonuc
def mergesort(arr):
	if len(arr) < 2:
		return arr
	orta = len(arr)//2
	sol = mergesort(arr[:orta])
	sag = mergesort(arr[orta:])

	return merge(sol, sag)

5. Hızlı Sıralama (Quick Sort)

Şu ana kadar bilinen en gözde ev hızlı algoritmadır. Uygulama adımlarını şu şekilde sıralayabiliriz:

• Diziden herhangi bir eleman al(pivot elaman)
• Pivot elemanından küçük olanları bir diziye, büyükleri bir diziye topla.
• Bu alt dizilerden yukarıdaki gibi pivot elemanları seçip aynı işlemi uygula. İç içe en küçük parçalara ulaşana kadar bu yöntemi sürdür.
• Oluşan dizicikleri birleştir

def parcalama(arr,low,high): 
    i = (low-1)       
    pivot_deger = arr[high]    
    for j in range(low , high): 
        if(arr[j] < pivot_deger): 
            i = i+1 
            arr[i],arr[j] = arr[j],arr[i] 
    arr[i+1],arr[high] = arr[high],arr[i+1] 
    return ( i+1 ) 
  
def quickSort(arr,low,high): 
    if(low < high): 
        pivot_deger = parcalama(arr,low,high) 
        quickSort(arr, low, pivot_deger-1) 
        quickSort(arr, pivot_deger+1, high) 
        
quickSort(arr,0,len(arr)-1)

Sıralama Algoritmalarının Karşılaştırılması

Sık kullanılan sıralama algoritmalarının, verinin karmaşıklığına göre gösterdiği performans:

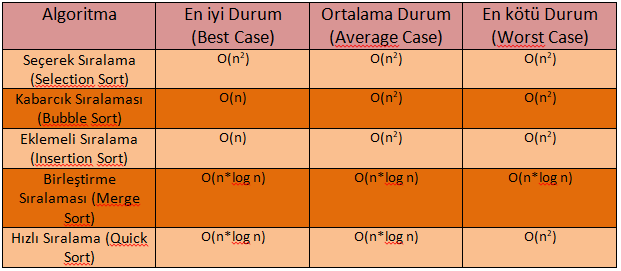
Kaynakça: Bilgisayarkavramlari, Teknoloji, Researchgate, Enacademic, SerdarKuzucu, Medium