Graf Teorisi

Graf teorisi elini kaldırmadan çizmeyi birçoğumuz ilkokul yıllarımızda karşılaşmışızdır. Ya arkadaşlarımız bizlere yada bizler onlara resimdeki şekli hiç el kaldırmadan çizip çizemeyeceğini sormuşuzdur. Hepimiz birkaç denemeden sonra sonucuna ulaşmışızdır. Ancak hiçbirimiz bunun aslında çok basit bir Matematik problemi olduğu bilmiyorduk.

Graf Nedir?

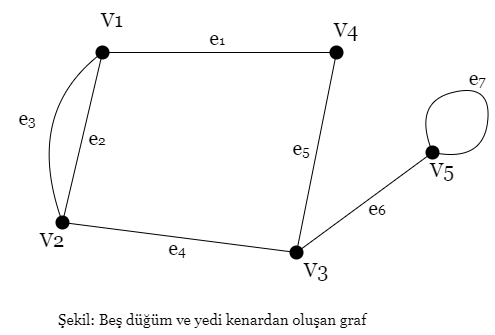
Bir graf G = (V,E) kümelerinden oluşur. Burada V = {v₁,v₂,…} kümesinin elemanlarına düğüm; E = {e₁,e₂ ,…} kümesinin elemanlarına da kenar adı verilir. Bir e_k kenarı sırasız bir çift (v_i, v_j) ile belirlenir. Sözü edilen v_i ve v_j düğümleri e_k kenarının başlangıç ve bitiş düğümleridir. Grafların en yaygın gösterimi şekilde gösterildiği gibi, düğümlerin birer nokta, kenarların ise kendi başlangıç ve bitiş düğümleri arasında doğru parçaları ile gösterildiği diyagramlardır. Diyagramın kendisi graf olarak olarak adlandırılır.

Bir grafta, herhangi bir e_k kenarı bir (v_i, v_j) düğüm çifti ile eşleşir. Başlangıç ve bitiş düğümleri aynı olan kenar döngü olarak adlandırılır. Şekilde e₇ kenarı bir döngüdür. Başlangıç ve bitiş düğümü aynı olan birden fazla kenar var ise bu kenarlara paralel denir. Şekilde e₂ ve e₃ kenarları paraleldir.

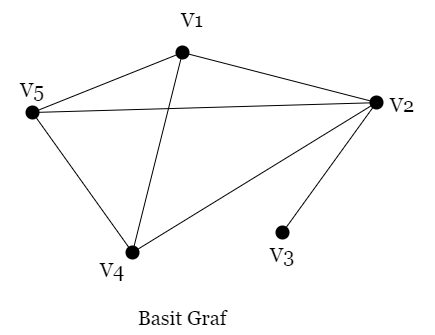
Basit (Simple) Graf

Aynı iki düğümün sadece bir hatla bağlandığı, herhangi bir düğümü yine kendisine bağlayan bir hattın (çevrimin) olmadığı, hatların bir değer almadığı ve yönünün tanımlanmadığı, düğüm ve hatların sınıflandırılmadığı graflara basit graf denir.

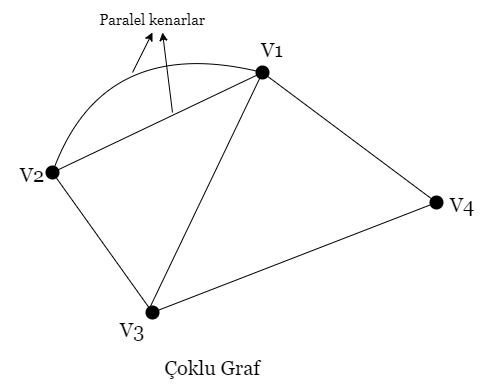
Çoklu (Multi) Graf

İki yada daha fazla düğüm arasında birden fazla hat (paralel hatlar) varsa bu tür graflara çoklu (multi) graf denir. Çoklu graflar da yönsüz ve çevrimsizdir. Örneğin iki şehir arasında iki farklı yol varsa, bu durum çoklu grafla temsil edilir.

Dipnot: Basit graflar, çoklu graftir fakat çoklu graflar basit graf degildir.

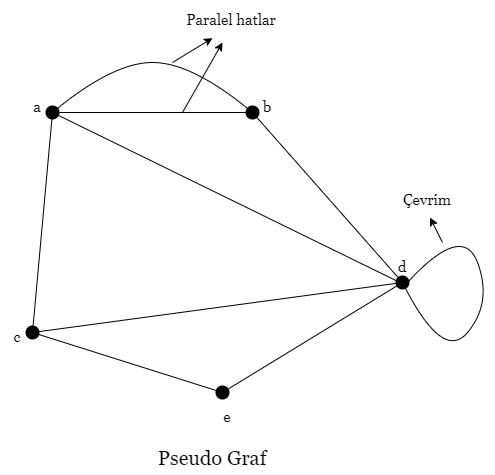
Pseudo Graf

Çoklu grafların yeterli olmadığı durumlarda kullanılır. Yönsüz, paralel kenarı olan ve döngü içeren graflardır. Yönsüz grafların en temel halidir.

Yönlü Graf

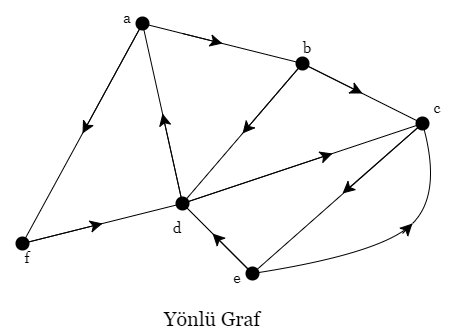
Bir graftaki hatlar yön bilgisine sahipse bu tür graflara yönlü graf (Directed graph) denir. Bu yön bilgisi bağlantının nereden başlayıp nereden bittiğini belirtir. Yön bilgisi olan graflarda düğümler arasındaki bağlantının yönü vardır.

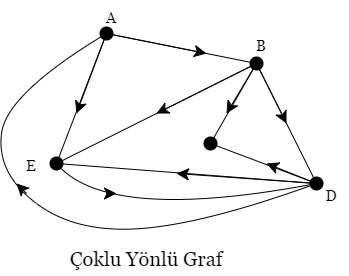
Çoklu Yönlü Graf

İki yönde bağlantı varsa ters yönde iki ayrı hat kullanılır ve bu tür graflara çoklu yönlü graf denir. Graf yapısında bütün kenarlar aynı çeşittir. Yani ya hepsi yönlüdür ya da değildir. Yol ağını temsil eden bir grafta trafiğin tek yada çift yönlü oluşu yönlü graflar için birörnektir.

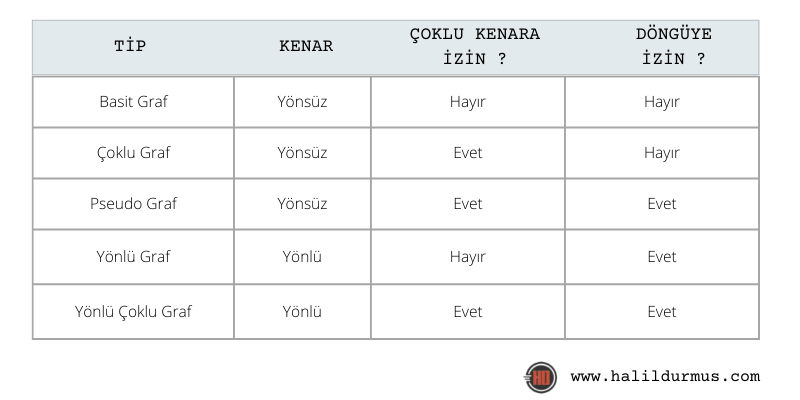
Grafların Karşılaştırılması

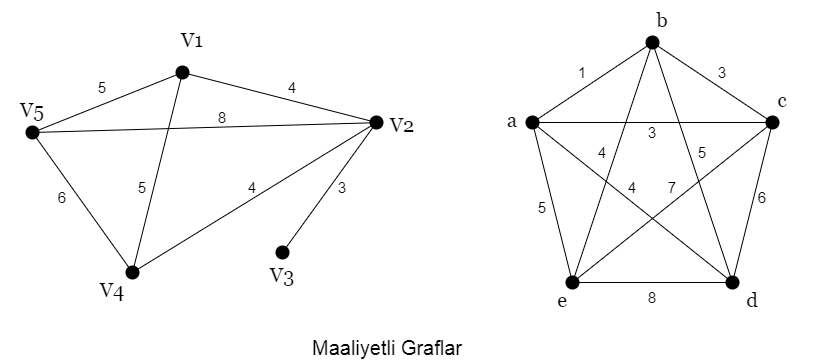
Maaliyetli (Ağırlıklı) Graf

Graf yapısındaki hatlar değer alabilir ve bu değerler grafın yapısına katılabilir. Aşağıdaki örnekte olduğu gibi, bir grafın üzerindeki hatların değerleri eşit değilse ve her biri farklı bir değer alabiliyorsa bu tip graflara maliyetli yada ağırlıklı graf (weighted graph) denir. Bütün hatların değeri aynı ise bu graf maliyetli graf olarak anılamaz. Ağırlıkların bir anlamı yoktur ve her hattın değerinin 1 olduğu basit graf gibi değerlendirilir. Şehirlerin arasındaki mesafelerin hatlara değer olarak atandığı yol haritasını temsil eden graflar maliyetli graflar için örnek verilebilir.

Düzlemsel Graf

Soldaki graf, kesişmeyen hatlardan oluşacak şekilde sağdaki gibi de çizilebilir. Bu şekilde birbirini kesmeyen hatlardan oluşacak şekilde çizilebilen graflara düzlemsel graf denir